
Käesolevat artiklit optimaalse laoseisu puhver- ja turvavaru teemal ajendas mind kirjutama üks diplomitöö. Selles arvutati toormaterjalide laovaru suurust ühe Eesti suure tootmisettevõtte tarvis. Kergelt kripeldama jäi aga see, et töö tulemusena soovitati ettevõttele kuus korda suuremaid toorainevarusid, kui tegelikkuses tarvis oleks olnud.
Aga nagu Eesti vanasõna ütleb: kus viga näed laita, tule ja aita. Seetõttu võtangi artikliga eesmärgiks teha puust ja punaseks, kuidas laoseisu puhver- ja turvavaru arvutusi üldtunnustatud valemite abil tehakse.
Esmalt, miks seda üldse vaja on?
Sobiva laoseisu määramine on üks olulisemaid ja keerulisemaid ülesandeid, millega protsesside eest vastutavad juhid kokku peavad puutuma.
Argumenti selleks ei pea kaugelt otsima. Kui ettevõttel on süsteemis liiga palju varusid, siis on käibekapitalist suur osa selle all kinni, samas kui varusid pole piisavalt, on tulemuseks OOS (out-of-stock). Potentsiaalne müük jääb teostamata või protsessides tekivad seisakud.
Et eeltoodu ei realiseeruks, siis optimaalne laoseis määratakse pealtnäha lihtsa valemiga: tsüklivarule tuleb liita puhver- ja turvavaru. Selle valemi tsüklivarude (varude hulk täiendamiste vahel) komponent on õnneks samuti kergemat sorti arvutus: keskmine nõudlus × täiendamise aeg.
Korralikku peavalu tekitab algajatel aga puhver- ja turvavaru (inglise keeles vastavalt buffer stock ja safety stock, kuigi paljudel juhtudel kutsutakse mõlemat koondatult ka safety stock‘ks) arvutamine.
Mis on laoseisu puhver- ja turvavaru?
Nii puhver- kui ka turvavaru on vajalikud, et katta OOS (out-of-stock) -olukordade teket, mis on tavaliselt põhjustatud kliendinõudluse või tarnete variatiivsusest, ennustustäpsusest, tootmisprotsesside stabiilsusest jne.
Kui nüüd veelgi rohkem detaili minna, siis puhvervaru on täpsemalt mõeldud/arvutatud nõudluse variatsiooni katmiseks ja turvavaru omakorda täiendamiste (näiteks tarnete õigeaegsuse) variatiivsuse kompenseerimiseks.
Üks sagedasemaid praktikaid puhver- ja turvavaru määramisel on kahjuks selle kõhutundelt otsustamine. Harvemal juhul arvutatakse see 10-20%-osakaaluna tsüklivarust või maksimaalse ja keskmise vahena nagu näiteks kirjeldatakse Virto Commerce veebilehele artiklis “How to calculate safety stock?“.
Eeltoodute plussiks on mõistagi lihtsus, kuid need on paraku kohutava sooritusega. Kui jätta kõhutundelt määramise lahendus välja (seda pole lihtsalt võimalik hetkel võrdluseks kalkuleerida), siis osakaalu ja max-avg arvutuste alusel leitud puhver- ja turvavaru kogused erinesid statistiliste meetoditega võrreldes suurusjärguna vastavalt 40% ja 60%.
Nii et need võib heaga ära unustada, sest ettevõttel tekiks sellise “täpsusega” palju probleeme, kuid eesmärgiks peaks olema siiski tasakaalu leidmine tarnekindluse (teenustaseme) ja laokulude vahel.
Kuidas puhver- ja turvavaru õigesti määrata?
Tasakaalu leidmisel tarnekindluse ja laokulude vahel peab arvestama, et mõlemat maksimaalselt saavutada ei ole võimalik. Nii tulebki juba eos arvestada, et kõiki OOS-olukordi pole võimalik optimaalsete kuludega vältida.
Näiteks kui kasutada statistilist lähenemist ja disainida laovaru 95% tarnekindluse peale (z-väärtus, mis näitab standardhälbe kaugust andmete keskväärtusest, oleks sellisel juhul 1,645 standardhälvet), siis võib eeldada, et 50% tõenäosusega saab hakkama määratud tsüklivaruga, 45% juhtudel läheb tarvis puhver- või turvavaru ja 5% kordadel tuleks arvestada, et nõudluse täitmiseks puuduvad ettevõttel varud (vaata skeemi all).
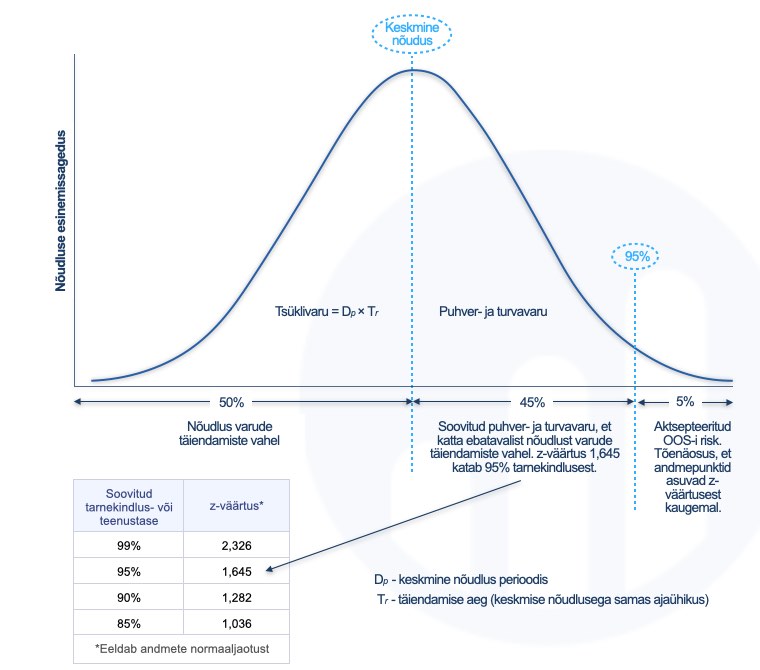
Kui OOS-ide vältimiseks tõsta tarnekindluse (või teenus-) taset veelgi, näiteks 99% nivooni (z-väärtus 2,326), siis esineks küll vähem olukordi, kus laost on midagi otsa saanud, kui nõuab jällegi rohkem puhver- ja turvavarusid. Ja mitte kõigest proportsionaalselt rohkem, vaid progresseeruvalt nagu näitab ka allolev graafik.

Kui tarnekindlust (teenustaset) tõsta, siis kasvab ka puhver- ja turvavaru, kuna z-väärtust kasutatakse standardhälbe kordajana, et statistilise tõenäosusega selgitada välja varude kogus ettenähtud taseme puhuks.
Et varud ei kujuneks liiga suureks, kuid samas tagada piisav tarnekindlus, siis teadlikumad ettevõtted sätivadki nivoo tavaliselt sinna 90%-98% vahele.
Puhvervaru arvutamine
Kui täiendamisajad on etteennustatavad ja variatsiooni ei esine (sellise stabiilse iseloomuga võiks olla näiteks täiendamine ettevõtte tsentraalsest laost), kuid nõudlus seevastu on juhuslikku laadi, siis võib puhvervaru (mis katab nõudluse variatiivsust) arvutada järgmise (ühest paljudest) valemi abil.
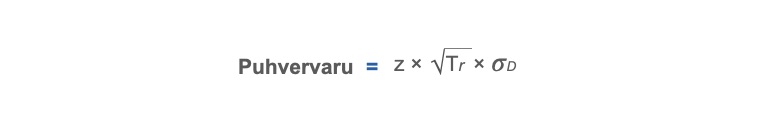
z – z-väärtus, millega määratakse valemis tarnekindluse (teenustaseme) määr
Tr – täiendamisele kuluv aeg (nõudlusega sama ajaühik)
𝜎D – nõudluse standardhälve (täiendamistega sama ajaühik)
Täiendamisaja puhul on oluline, et kasutatakse reaalset aega. Näiteks kui täiendamine võtab aega 30 minutit, kuid seda tehakse transpordi mastaabisäästu huvides vaid korra nädala jooksul, siis ei ole täiendamise aeg eelmainitud pool tundi, vaid 7 päeva.
Teeme arvutuse ka praktiliselt läbi. Oletame, et ettevõtte tootmisjuht soovib teada, kui suur peaks toote XS100 nõudluse variatsiooni katmiseks olema laoseisu puhvervaru osa olukorras, kus oma koostööpartnerid (kliendid) nõuavad 95% tarnekindlust ja täiendamine (XS100 valmistamine) võtab aega ilma igasuguse variatsioonita 2 päeva.
95% tarnekindluse tagamiseks peame arvutuses kasutama z-väärtust 1,645.
Nõudluse standardhälbe saame varasema ajaloo põhjal järgmiselt.

Müügikoguste standardhälve viimase 30 päeva ajaloo põhjal on 3,7. Siinkohal tasub tähele panna, et standardhälbe arvutamisel ei satuks andmete hulka erinevad hooajalisused. Arvutada tuleks need konkreetse (madala või kõrge) hooaja kohta.
Nüüd on meil olemas kõik andmed, et arvutada puhvervaru hulka.
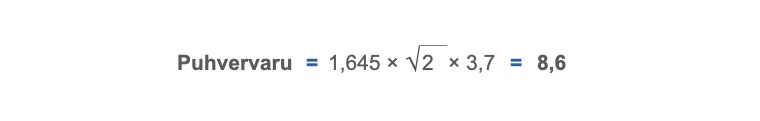
Siit edasi on juba lihtne leida kogu laovaru suurus täiendamistsükli katmiseks (lean-juhtimises kutsutud ka kanban-koguseks). Tsüklivarule (keskmine nõudlus × täiendamise aeg) tuleb liita puhvervaru.

Turvavaru arvutamine
Eelnevalt arvutasime puhvervaru, mis oli mõeldud nõudluse variatiivsuse katmiseks. Kui aga peamiseks probleemiks on täiendamisaja (tarneaja) varieerumine, siis tuleks järgmise valemi abil arvutada hoopis turvavaru.

z – z-väärtus, millega määratakse valemis tarnekindluse (teenustaseme) määr
𝜎Tr – täiendamiste standardhälve (keskmise nõudlusega sama ajaühik)
Davg – keskmine nõudlus (täiendamistega sama ajaühik)
Teeme ka turvavaru arvutuse näite varal läbi. Oletame, et ettevõtte tootmisjuht soovib teada, kui suur peaks olema toote XS100 koostedetaili XEN15 laoseisu turvavaru osa. Neid valmistava alltöövõtja tarnekindlus lubatud 14 päeva osas on kahjuks ebastabiilne ja on põhjustanud mitmel korral tootmisseisakuid.
Tootmisjuht tahab aga seda vältida ja tagada selle detaili saadavusmäära 98% ulatuses, ja seda olukorras, kus XS100 (järelikult ka XEN15 detaili, kui koosteprobleeme ei esine) keskmine nõudlus on 15,63 tk päevas.
98% tarnekindluse tagamiseks peame arvutuses kasutama z-väärtust 2,053.
Detaili XEN15 täiendamiste (alltöövõtja tarnete) standardhälbe saame varasema ajaloo põhjal järgmiselt.
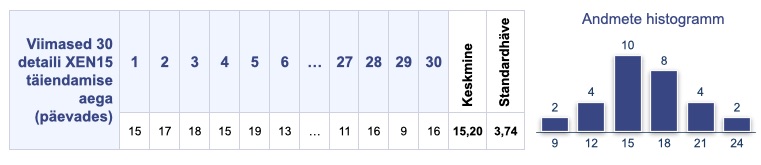
Tarnete standardhälve viimase 30 päevase ajaloo põhjal on 3,74. Ja nüüd on meil olemas kõik andmed turvavaru arvutamiseks.
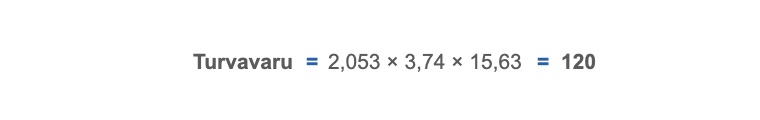
Kogu laovaru suurus, et katta täiendamistsüklit ebastabiilselt tarnijalt, kujuneks eeltoodud andmete põhjal järgmiseks.

Aga kui esinevad mõlemad: nii nõudluse kui ka tarnete variatsioon?
Võib juhtuda (tegelikult nii tavaliselt ongi), et laovaru määramisel peame arvestama mõlema variatsiooniga, nii nõudluse kui ka täiendamisaegade omaga.
Kui nõudluse ja täiendamisaja variatsioon on üksteisesest sõltuvad, näiteks täiendamise aeg mõjutab nõudlust või vastupidi, ja andmed järgivad normaaljaotust, siis tuleks eeltoodud puhver-ja turvavaru arvutuste tulemused omavahel liita.
Kui nõudluse ja täiendamisaja variatsioon on aga üksteisest sõltumatud, ehk et nad on mõjutatud erinevate tegurite poolt, ja mõlema andmed järgivad normaaljaotust, siis tasuks arvutust kombineerida. See annab tulemuseks mõnevõrra väiksema varu hulga (täpsema), kui kaks eraldi arvutust omavahel liita.
Kombineeritud puhver- ja turvavaru arvutatakse järgmise valemiga.
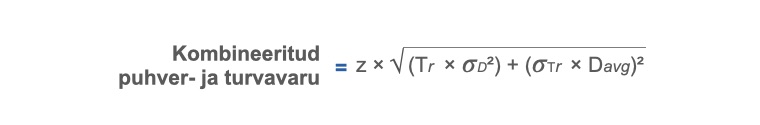
Teeme arvutuse ka praktiliselt läbi juba eelnevalt kasutatud andmetega, kus toote XS100 koostööpartnerid (kliendid) nõuavad 95% tarnekindlust, täiendamisaeg on 15,2 päeva standardhälbega 3,72 ja keskmine nõudlus 15,63 tk/päevas standardhälbega 3,7.
Tulemuseks saame ümardatult 99tk, mis peaks meid lisaks tsüklivarule ebastabiilsuse eest kaitsma.
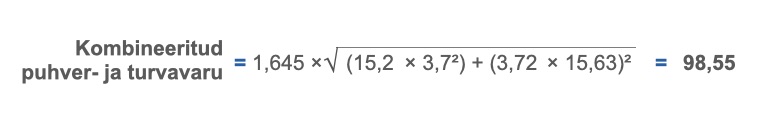
Kogu laovaru suurus, et katta täiendamistsüklit nii nõudluse kui ka tarneaja variatsiooni korral, kujuneks eelkäsitletud andmete põhjal järgmiseks.

Kokkuvõtteks
Eeltoodud valemid baseerusid tõenäosusteoorial ja olukordades, kus nõudluse ja täiendamise andmed järgivad normaaljaotust. Üldjuhul on sellisteks valmiskauba, toorainete ja pooltoodetega seotud andmed.
Aga näiteks ettevõttes toodetud, kuid vahepeal muu partneri juures lisatöötlust saanud artiklite andmed normaalselt siiski ei jaotu ning siinkäsitletud valemeid rakendada ei saa.
Lisaks toovad tootmismatemaatikud W. J. Hopp ja M. L. Spearman eeltoodud statistikal baseeruvate valemite kitsaskohtadena välja ka selle, et kui nõudlus või täiendamine käib suurte partiidena, siis võivad puhver- ja turvavaru kogused olla pisut ebatäpsed.
Hoolimata kriitikast on eeltoodud valemid ja põhimõtted ikkagi kordades täpsemad puhver- ja turvavaru koguste hindamisel, kui seda on kõhutundelt otsustamine või suhtarvuline määramine.


